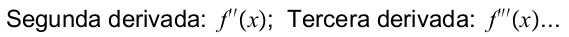Después de haber entendido qué son las derivadas, vamos a aprender a calcularlas. Para hallar la derivada de una función normalmente se recurre a un conjunto de reglas que uno debe dominar tan bien como las tablas de multiplicar para operar con agilidad. Las principales reglas de derivación son:
1.-Derivada de una función constante
La derivada de una función constante es 0, ya que la variable dependiente toma siempre el mismo valor. La variación es nula.
2.-Derivada de la función identidad
La función identidad es una función lineal, por lo que su pendiente no cambia (en este caso es 1). Por lo tanto, en todos los puntos de esta función la derivada es la misma, esa pendiente.
3.-Derivada de una función afín
Ocurre lo mismo que con las funciones lineales. La pendiente, y así también la derivada, de una función afín es fija.
4.-Derivada de una función potencial
La derivada de una función potencial es igual al producto del exponente de la potencia por la base x elevada al exponente inicial menos 1.
5.-Derivada de una función exponencial
La derivada de una función exponencial es igual a la potencia multiplicada por el logaritmo neperiano de la base.
6.-Derivada de una función exponencial con el número e como base
Siguiendo la regla anterior, al hacer esta derivada multiplicaríamos la potencia por el logaritmo neperiano de la base. Como esta base es el número e, ese logaritmo neperiano vale 1, de manera que podemos resumir diciendo que la derivada de esta función exponencial es ella misma.
7.-Derivada de una función logarítmica
La derivada de un logaritmo en base a de x es igual a 1/x por el logaritmo en base a del número e.
8.-Derivada de un logaritmo neperiano
Si aplicamos la regla de antes, tenemos que multiplicar 1/x por el logaritmo en base a del número e. Como la base a es en este caso el número e, tenemos el logaritmo neperiano de e, que vale 1. Por eso el resultado final de esta derivada es 1/x.
9.-Derivada del seno
La derivada de la función seno de x es igual a otra función trigonométrica: el coseno de x.
10.-Derivada del coseno
La derivada de la función coseno de x es igual al seno negativo de x.
11.-Derivada de la tangente
La derivada de la función tangente de x es igual a 1 más tangente al cuadrado de x, que es lo mismo que dividir 1 entre el coseno al cuadrado de x.
12.-Derivada de una suma
La derivada de una suma de funciones es igual a la suma de sus derivadas.
13.-Derivada de un producto
La derivada de un producto de funciones es igual a la derivada de la primera por la segunda sin derivar más la primera sin derivar por la derivada de la segunda.
14.-Derivada de un cociente
La derivada de un cociente de funciones, g entre h, es igual a otro cociente. El numerador de este es igual a la derivada de g por h sin derivar menos g sin derivar por la derivada de h. En cuanto al denominador del nuevo cociente, será la función h elevada al cuadrado.
15.-Derivada de una composición de funciones
La derivada de una composición de dos funciones es igual a la derivada de la primera por la derivada de la segunda, la que hemos introducido en la anterior.
16.-Derivada de una función elevada a otra función
La derivada de una función g elevada a otra función h es igual a h multiplicada por g elevada a h-1 y por la derivada de g, más la derivada de h por g elevada a h.
Notación
Otro punto que nos interesa repasar después de las reglas de derivación es la notación. Además de la que hemos utilizado, existen otras formas de señalar que vamos a realizar una derivada. Estas son las más usuales:
Regla de la cadena
A la hora de derivar también es muy importante dominar la regla de la cadena. Para entenderla, supongamos que y es función de u, y que u es función de x:
Entonces se dice que y es una función compuesta de x. Imaginemos ahora que el valor de x cambia. Esto provocará un cambio en el valor de u y, por lo tanto, también en el de y. Es decir, el cambio en x causa una especie de reacción en cadena que termina afectando a y. Para cuantificar ese cambio utilizamos la regla de la cadena, según la cual si y es una función derivable de u, y u es una función derivable de x, entonces y es una función derivable de x y esta derivada viene dada por:
Derivar una derivada
Tampoco hay que olvidar que la derivación es una operación que podemos realizar tantas veces seguidas como sea posible. En realidad, la derivada de una función es también una función, por lo que cabe la posibilidad de que también sea derivable. Así, a la derivada de la derivada se la conoce como segunda derivada, a la derivada de esta la llamaremos tercera derivada, y así sucesivamente:
Nos detenemos aquí. Continuaremos en el próximo capítulo con varios ejemplos para completar este repaso a las derivadas.
CONTINUARÁ...
BIBLIOGRAFÍA
- Clases de Matemáticas I de la Prof. Dra. Haydée Corina Lugo Arocha (Universidad Complutense de Madrid).
- Clases de Matemáticas Aplicadas a las Ciencias Sociales del Prof. Segundo García-Risco Sánchez (IES Muñoz-Torrero de Cabeza del Buey).
- GARCÍA PINEDA, P.; NÚÑEZ DEL PRADO, J.A.; GÓMEZ SEBASTIÁN, A. (2007): Iniciación a la Matemática Universitaria, Thomson, Madrid.
- SYDSAETER, K.; HAMMOND, P.; CARVAJAL, A. (2012): Matemáticas para el Análisis Económico, Pearson, Madrid.
Autor:
Manuel V. Montesinos